45 Dynamical systems
We will need some of the theory from your prior ODEs and Modelling and Dynamics courses as related to the solution of 2x2 linear systems of the form \[ \mathbf{Y}'(t) = \mathbf{A}(t) \mathbf{Y}, \] where \[ \mathbf{Y}(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix}, \quad \text{and} \quad \mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \]
If you need a refresher, refer to your old notes; there is also a good review on these notes and also these notes.
45.1 Stability analysis for 2x2 systems
In the case of 2x2 systems, there is a useful classification and shortcut. The eigenvalues, \(\lambda_1\) and \(\lambda_2\) are given by \[ \lambda_{1,2} = \frac{1}{2} (T \pm \sqrt{T^2 - 4D}), \] where \(T = \mathrm{tr}(A) = a + d\) and \(D = \mathrm{det}(A) = ad - bc\). Once \(T\) and \(D\) are known, then the fixed points can be classified based on the following diagram.
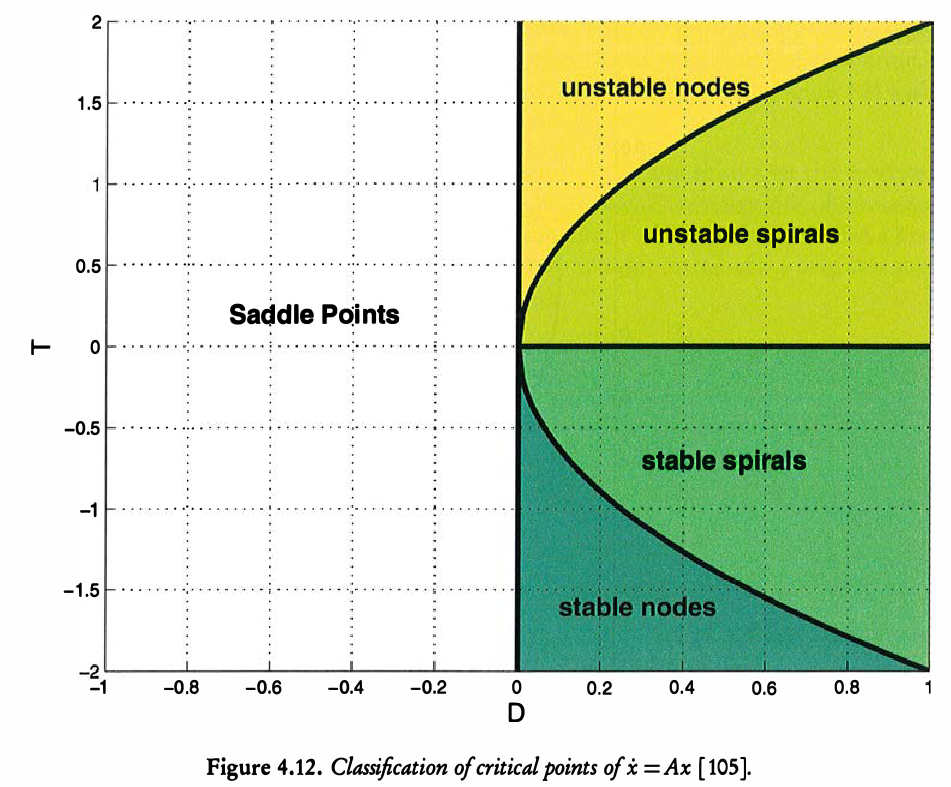
Above, the critical parabola is where \(T^2 - 4D = 0\).