Conservation of mass

Section 3.2 Conservation of mass

Our task from this section is to prove the following equation for the conservation of mass of a fluid:

🔗

Theorem 3.2.1. Continuity equation.

The differential form of the law of conservation of mass, otherwise known as the continuity equation is

\begin{equation} \pd{\rho}{t} + \nabla \cdot (\rho \bu) = 0,\tag{3.2.1} \end{equation}

where $\rho = \rho(\bx,t)$ is the density of the fluid and $\bu = \bu(\bx, t)$ is the velocity of the fluid.

🔗

The above form is equivalent, by the definition of the convective derivative, to

\begin{equation} \DD{\rho}{t} + \rho(\nabla \cdot \bu) = 0.\tag{3.2.2} \end{equation}

🔗

In fact, as it turns out, the proof of this result is trivial if we use the Reynolds’ Transport Theorem and Lagrangian formulation following Theorem 3.1.3.

🔗

Proof.

We consider the time differentiation of the mass integral,

\begin{equation*} \iiint_{V(t)} \rho \, \de{V}, \end{equation*}

for an arbitrary material volume $V(t)$ in the fluid.

🔗

By Theorem 3.1.3, we can use the Reynolds’ Transport Theorem to pass the time derivative through the integral. This gives:

\begin{equation*} \dd{}{t}\iiint_{V(t)} \rho \de{V} = \iiint_{V(t)} \left[ \pd{\rho}{t} + \nabla \cdot (\rho \bu)\right] \, \de{V}, \end{equation*}

which is satisfied for any volume $V \subseteq D$ where the fluid is defined. Since the result is true for any such possible volume, then the integrand of the right hand-side, itself, must be zero. This gives immediately (3.2.1).

🔗

The proof of (3.2.2) follows immediately from application of the definition of the convective derivative (2.1.1).

🔗

Within the above proof, we use an idea used throughout this chapter, which is that if an integral of a quantity (the integrand) is zero for all possible domains of integration, then the integrand, itself, is zero. This is sometimes referred to as the "Bump lemma".

🔗

Lemma 3.2.2. Bump lemma.

Let $f(\bx)$ be a sufficiently smooth function defined on $\Omega \subseteq \mathbb{R}^n\text{.}$ Suppose it is the case that

\begin{equation*} \int_V f(\bx) \, \de{V} = 0, \end{equation*}

for all $V \subseteq \Omega\text{.}$ Then

\begin{equation*} f(\bx) \equiv 0 \end{equation*}

in $\Omega\text{.}$

🔗

In Exercise 3.6.2, you will prove the above lemma.

🔗

Subsection 3.2.1 Derivation of mass conservation using Eulerian methods

The derivation we have just shown for Theorem 3.2.1, using the Lagrangian viewpoint and the Reynolds’ Transport Theorem is misleadingly simple, and it can be instructive to see how the result is proved purely from the perspective of Eulerian coordinates.

🔗

For this, let us consider $V$ to be a fixed and closed subregion of the overall fluid, $D$ that does not change with time. An illustration of this is shown in Figure 3.2.3.

🔗

We want to prove the following result, which essentially equates the change in mass, due to density changes, to the flow of mass in or out of the volume.

🔗

Theorem 3.2.4. Integral form of the law of conservation of mass.

Given a fixed volume element $V$ and boundary $\partial V\text{,}$ the integral form of the law of mass conservation is

\begin{equation} \dd{}{t} \iiint_V \rho \, \de{V} = -\iint_{\partial V} \rho \bu \cdot \bn \, \de{S}.\tag{3.2.3} \end{equation}

🔗

Proof.

The rate of change of mass in $V$ is

\begin{equation*} \dd{}{t} \iiint_V \rho(\bx, t) \, \de V = \iiint_V \pd{\rho}{t} \, \de V, \end{equation*}

and note the derivative passes through the integral since the volume, $V\text{,}$ does not change with time.

🔗

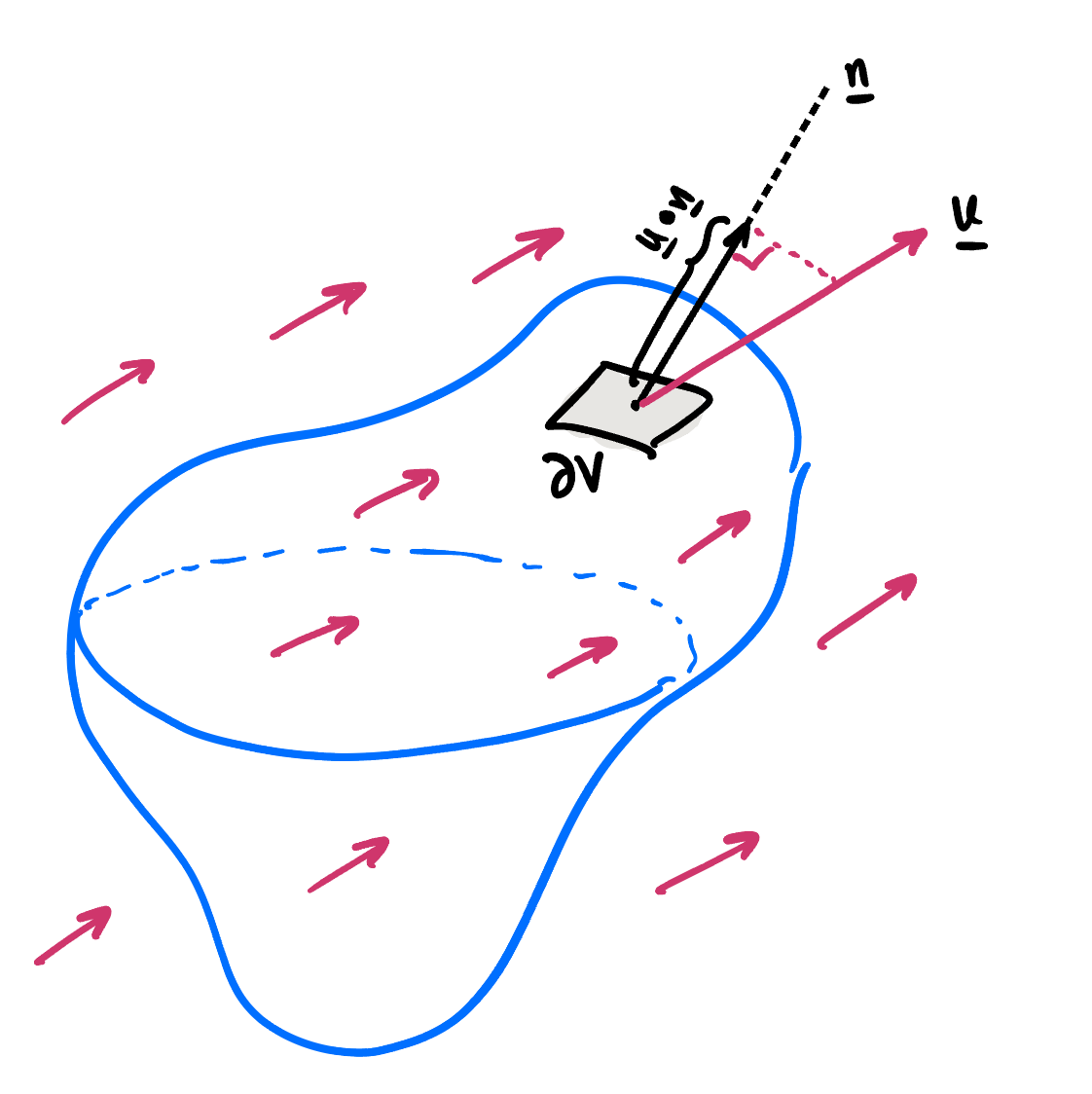
Let the boundary of $V$ be given by $\partial V\text{,}$ and let $\bn$ denote the outward unit normal defined along the boundary $\partial V\text{.}$ At each point on the boundary, the volume flow rate (known as the flux) across the boundary is given by $\bu \cdot \bn$ and therefore the mass flow rate is $\rho \bu \cdot \bn\text{.}$

🔗

We now sum the total mass flow across the entire boundary. This is given by the surface integral

\begin{equation*} \text{rate of mass change across $\partial V$} = \iint_{\partial V} \rho \bu \cdot \bn \, \de{S}. \end{equation*}

The flux out of the boundary is also sketched in Figure 3.2.3.

🔗

Mass conservation is now applied. Therefore, the rate of change of pass in the volume $V$ is equal to the rate at which mass enters the boundary in the inwards direction.

🔗

We now want to transform the integral form in (3.2.3) into the form of a partial differential equation. To do this, apply the Divergence theorem to the right hand-side of the above integral, converting the surface integral to a volume integral. Moving all quantities to the left hand side now yields

\begin{equation*} \iiint_V \left[ \pd{\rho}{t} + \nabla \cdot (\rho \bu)\right] \, \de{V} = 0. \end{equation*}

Since the above integral equation holds for all possible $V\text{,}$ it must be equivalent to the integrand equated to zero (Lemma 3.2.2). This yields our final result leading to Theorem 3.2.1.

🔗

Subsection 3.2.2 Corollary of the Transport Theorem

Corollary 3.2.5.

There is a useful corollary to the transport theorem in Theorem 3.1.3 in the case where the desired function of integration, $f\text{,}$ is proportional to the density, i.e. $f = \rho h$ for any continuously differentiable $h\text{.}$ Indeed consider a moving volume $V(t)\text{,}$ and a density $\rho$ that satisfies the continuity equation (3.2.1) or (3.2.2).

🔗

Then

\begin{equation} \dd{}{t} \iiint_{V(t)} \rho h \, \de{V} = \iiint_{V(t)} \rho \DD{h}{t} \, \de{V}.\tag{3.2.4} \end{equation}

🔗

Proof.

This proof just follows from expansion. Pass the derivative through the integral and use the Reynolds’ transport theorem formula. Then expand the quantity:

\begin{equation*} \nabla \cdot (f\bu) = \nabla f \cdot \bu + f \nabla \cdot \bu. \end{equation*}

where $f = \rho h\text{.}$ Finally use the continuity equation on $\rho\text{.}$

🔗

Prev Top Next