Exercises

Exercises 6.5 Exercises

1. Kelvin’s Circulation Theorem.

The circulation \(\Gamma\) around a closed curve \(C(t)\) is defined by

\begin{equation*} \Gamma = \oint_{C} \mathbf{u} \cdot \de\mathbf{x}. \end{equation*}

By transforming to Lagrangian variables show that \(\Gamma\) is independent of \(t\text{.}\) Deduce that a flow that is initially irrotational (i.e. \(\bomega = 0\) at \(t=0\)) remains irrotational for all time.

🔗

Note that this is a key result: if a flow is initially irrotational, it remains so indefinitely and we can introduce a velocity potential \(\phi\) such that \(\mathbf{u} = \nabla \phi\text{.}\)

🔗

Hint.

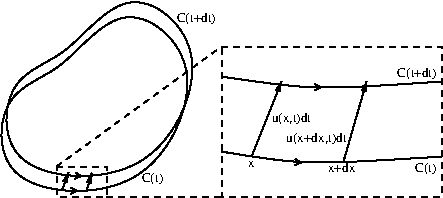
Method one: Consider the following diagram.

🔗

Figure 6.5.1. Curve \(\Gamma\) at times \(t\) and \(t+\de t\text{.}\) The inset shows the relationship between the two curves.
🔗

By definition,

\begin{equation} \dd{\Gamma}{t}=\lim_{\de t\rightarrow0}\frac1{\de t}\left(\oint_{C(t+\de t)}\bu\cdot\de\bx-\oint_{C(t)}\bu\cdot\de\bx\right).\tag{6.5.1} \end{equation}

We therefore need to write \(\bu\) and \(\de\bx\) at time \(t+\de t\) on the curve \(C(t+\de t)\) to values at time \(t\) on the curve \(C(t)\text{:}\)

\begin{align*} &\left.\bu\cdot\de\bx\right|_{t+\de t}\\ =&\bu(\bx+\bu(\bx,t)\de t,t+\de t)\cdot\\ &\left((\bx+\de\bx+\bu(\bx+\de\bx,t)\de t)-(\bx+\bu(\bx,t)\de t)\right). \end{align*}

🔗

Method two: We can parametrise \(C(t)\) via \(\bx(s,t)\) for \(0<s<1\) and rewrite the integral as an integral over the parameter \(s\text{:}\)

\begin{equation*} \Gamma=\int_0^1\bu(\bx(s,t),t)\cdot\pd{\bx(s,t)}{s}\de s \end{equation*}

Then start from (6.5.1) and simplify.

🔗

Solution.

We present two methods.

🔗

Method one:

🔗

Assuming a conservative body force \(-\bnabla\chi\) per unit volume, the Euler equation reads

\begin{equation*} \DD{\bu}{t}=-\bnabla\left(\frac{p}{\rho}-\chi\right). \end{equation*}

We have

\begin{equation*} \dd{\Gamma}{t}=\lim_{\de t\rightarrow0}\frac1{\de t}\oint_C\left(\bu\cdot(\de\bx\cdot\bnabla)\bu-\bnabla\left(\frac{p}{\rho}-\chi\right)\cdot\de\bx\right)\de t. \end{equation*}

We calculate

\begin{align*} \left.\bu\cdot\de\bx\right|_{t+\de t}=&\bu(\bx+\bu(\bx,t)\de t,t+\de t)\cdot\\ &\left((\bx+\de\bx+\bu(\bx+\de\bx,t)\de t)-(\bx+\bu(\bx,t)\de t)\right)\\ =&\left(\bu(\bx,t)-\bnabla\left(\frac{p}{\rho}-\chi\right)\de t\right)\cdot\left(\de\bx+(\de\bx\cdot\bnabla)\bu\de t\right)\\ =&\left.\bu\cdot\de\bx\right|_{t}+\left(\bu\cdot(\de\bx\cdot\bnabla)\bu-\bnabla\left(\frac{p}{\rho}-\chi\right)\cdot\de\bx\right)\de t. \end{align*}

Hence

\begin{align*} \dd{\Gamma}{t}&=\lim_{\de t\rightarrow0}\frac1{\de t}\oint_C\left(\bu\cdot(\de\bx\cdot\bnabla)\bu-\bnabla\left(\frac{p}{\rho}-\chi\right)\cdot\de\bx\right)\de t\\ &=\oint_C\bu\cdot(\de\bx\cdot\bnabla)\bu-\bnabla\left(\frac{p}{\rho}-\chi\right)\cdot\de\bx\\ &=\oint_C\bnabla\left(\frac12\bu^2\right)\cdot\de\bx-\bnabla\left(\frac{p}{\rho}+\chi\right)\cdot\de\bx\\ &=\oint_C\bnabla\left(\frac12\bu^2-\frac{p}{\rho}-\chi\right)\cdot\de\bx\\ &=0. \end{align*}

The final equality above follows because the line integral of a gradient around a closed curve is zero. Thus \(\Gamma\) is independent of \(t\text{.}\) If the flow is initially irrotational, then \(\Gamma=0\) at \(t=0\) for any closed curve \(C(0)\text{,}\) and hence \(\Gamma=0\) for all time. Since this holds for any closed curve, it follows that \(\omega=\bnabla\times\bu=0\) for all time.

🔗

Method two: This can also be proven by parametrising \(C(t)\) via \(\bx(s,t)\) for \(0<s<1\) and rewriting the integral as an integral over the parameter \(s\text{:}\)

\begin{equation*} \Gamma=\int_0^1\bu(\bx(s,t),t)\cdot\pd{\bx(s,t)}{s}\de s. \end{equation*}

Then

\begin{align*} \dd{\Gamma}{t}= &\int_0^1 \left.\pd{}{t}\left(\bu(\bx(s,t),t)\cdot\pd{\bx(s,t)}{s}\right)\right|_s\de s\\ =&\int_0^1 \left(\left(\pd{\bu}{t}+\pd{\bx}{t}\cdot\nabla\bu\right)\cdot\pd{\bx}{s} +\bu\cdot\pd{^2\bx}{s\partial t}\right)\de s\\ =&\int_0^1 \left(\left(\pd{\bu}{t}+\bu\cdot\nabla\bu\right)\cdot\pd{\bx}{s} +\bu\cdot\pd{\bu}{s}\right)\de s\\ =&\int_0^1\left(\DD{\bu}{t}\cdot\pd{\bx}{s}+\frac12\pd{|\bu|^2}{s}\right)\de s\\ =&\int_0^1\left(-\bnabla\left(\frac{p}{\rho}-\chi\right)\cdot\pd{\bx}{s}+\frac12\pd{|\bu|^2}{s}\right)\de s\\ =&\int_0^1\left(-\pd{}{s}\left(\frac{p}{\rho}-\chi\right)+\frac12\pd{|\bu|^2}{s}\right)\de s\\ =&0. \end{align*}

🔗

2. The circulation around a vortex tube.

(Based on Exercise 5.5 in [4]). Define a vortex tube. Prove that the quantity

\begin{equation*} \Gamma = \int_S\bomega\cdot\bn\,\de S, \end{equation*}

where \(S\) is any surface spanning the tube, is the same for all such surfaces. Relate this quantity to a circulation of the flow.

🔗

Hint.

Given two different such surfaces \(S_1\) and \(S_2\text{,}\) define a `cylindrical’ volume \(V\text{,}\) whose ends are the the two surfaces \(S_1\) and \(S_2\) and whose sides are the sides of the vortex tube, and let \(\Gamma_i = \int_{S_i}\bomega\cdot\bn_i\,\de S\text{,}\) for \(i=1,2\text{.}\)

🔗

Solution.

🔗

Consider \(\int_{\partial V}\bomega\cdot\bn\,\de S\text{.}\) This is equal to \(\Gamma_1\) minus \(\Gamma_2\) plus the integral of \(\bomega\cdot\bn\) over the sides of the cylinder. On the sides of the cylinder, we have \(\bomega\cdot\bn=0\text{.}\) Hence, \(\Gamma_1=\Gamma_2\) for any two such surfaces.

🔗

Stokes theorem implies that

\begin{equation*} \Gamma = \oint_C\bomega\times\de\bx, \end{equation*}

where \(C\) is the curve around the edge of \(S\text{,}\) which is the circulation.

🔗

Since the circulation is constant in time, this implies the flux of vorticity through any vortex tube is uniform and independent of time.

🔗

3. Evolution of a line integral.

(Based on Exercise 5.6 in [4]). Show that if \(\mathbf{a}(\bx,t)\) is any suitably smooth vector field and

\begin{equation*} \mathcal{C}(t)=\int_{C(t)}\mathbf{a}\cdot\de\bx, \end{equation*}

where \(C(t)\) is a circuit consisting of the same fluid particles as time proceeds, then

\begin{equation*} \dd{\mathcal{C}}{t}=\int_{C(t)} \left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx. \end{equation*}

🔗

Hint.

Similar to Exercise 6.5.1, there are two methods of solution possible.

🔗

First method:

🔗

Figure 6.5.2. Curve \(C\) at times \(t\) and \(t+\de t\text{.}\) The inset shows the relationship between the two curves.
🔗

We write

\begin{equation*} \dd{\mathcal{C}}{t}=\lim_{\de t\rightarrow0}\frac1{\de t} \left(\int_{C(t+\de t)}\mathbf{a}(\bx,t+\de t)\cdot\de\bx -\int_{C(t)}\mathbf{a}(\bx,t)\cdot\de\bx\right). \end{equation*}

🔗

Second method: Parametrise \(C(t)\) as \(\bx(s,t)\) for \(0<s<1\text{.}\) Then

\begin{equation*} \mathcal{C}(t)=\int_0^1\mathbf{a}\cdot\pd{\bx}{s}\de s. \end{equation*}

🔗

Solution.

We present two methods of solution.

🔗

First method:

🔗

Figure 6.5.3. Curve \(C\) at times \(t\) and \(t+\de t\text{.}\) The inset shows the relationship between the two curves.
🔗

We write

\begin{equation*} \dd{\mathcal{C}}{t}=\lim_{\de t\rightarrow0}\frac1{\de t} \left(\int_{C(t+\de t)}\mathbf{a}(\bx,t+\de t)\cdot\de\bx -\int_{C(t)}\mathbf{a}(\bx,t)\cdot\de\bx\right) \end{equation*}

and note that

\begin{align*} &\int_{C(t+\de t)}\mathbf{a}(\bx,t+\de t)\cdot\de\bx\\ =&\int_{C(t)}\mathbf{a}\left(\bx+\bu(x,t)\de t+\dots,t+\de t\right)\cdot \left(\bx+\de\bx+\bu(\bx+\de\bx,t)\de t-\bx-\bu(\bx,t)\de t\right)\\ =&\int_{C(t)}\left(\mathbf{a}(\bx,t)+\pd{\mathbf{a}}{t}(\bx,t)\de t +\bu(x,t)\cdot\nabla\mathbf{a}(\bx,t)\de t+\dots\right)\cdot \left(\de\bx+\left(\de\bx\cdot\nabla\right)\bu(\bx,t)\de t\right) \end{align*}

Hence

\begin{align*} \dd{\mathcal{C}}{t}=&\lim_{\de t\rightarrow0}\frac1{\de t} \int_{C(t)}\left( \mathbf{a}(\bx,t)\cdot\left(\left(\de\bx\cdot\nabla\right)\bu(\bx,t)\right)\de t +\pd{\mathbf{a}}{t}(\bx,t)\de t\cdot\de\bx +\left(\bu(\bx,t)\cdot\nabla\right)\mathbf{a}(\bx,t)\de t\cdot\de\bx +\dots\right)\\ =&\int_{C(t)}\left( \mathbf{a}\cdot\left(\left(\de\bx\cdot\nabla\right)\bu\right) +\pd{\mathbf{a}}{t}\cdot\de\bx +\left(\left(\bu\cdot\nabla\right)\mathbf{a}\right)\cdot\de\bx\right) \end{align*}

Now we use the identity

\begin{equation*} \left(\mathbf{p}\times\mathbf{q}\right)\times\mathbf{r} =\left(\mathbf{p}\cdot\mathbf{r}\right)\mathbf{q} -\left(\mathbf{q}\cdot\mathbf{r}\right)\mathbf{p} \end{equation*}

to expand

\begin{equation*} \left(\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx =\left(\left(\bu\cdot\nabla\right)\mathbf{a}\right)\cdot\de\bx -\bu\cdot\left(\left(\de\bx\cdot\nabla\right)\mathbf{a}\right). \end{equation*}

Hence

\begin{align*} \dd{\mathcal{C}}{t} -\int_{C(t)}\left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx =& \int_{C(t)} \mathbf{a}\cdot\left(\left(\de\bx\cdot\nabla\right)\bu\right) +\bu\cdot\left(\left(\de\bx\cdot\nabla\right)\mathbf{a}\right)\\ =&\int_{C(t)} \mathbf{a}\cdot\de\bu +\bu\cdot\de\mathbf{a}\\ =&\int_{C(t)} \de\left(\mathbf{a}\cdot\bu\right)\\ =&0, \end{align*}

whence the result.

🔗

Second method: Parametrise \(C(t)\) as \(\bx(s,t)\) for \(0<s<1\text{.}\) Then

\begin{equation*} \mathcal{C}(t)=\int_0^1\mathbf{a}\cdot\pd{\bx}{s}\de s \end{equation*}

Then

\begin{align*} \dd{\mathcal{C}}{t} =&\int_0^1\pd{\mathbf{a}(\bx(s,t),t)}{t}\cdot\pd{\bx}{s}+\mathbf{a}\cdot\pd{\bu}{s}\de s\\ =&\int_0^1\left(\pd{\mathbf{a}}{t}+\bu\cdot\nabla\mathbf{a}\right)\cdot\pd{\bx}{s}+\mathbf{a}\cdot\pd{\bu}{s}\de s. \end{align*}

We can rewrite the expression we are aiming for:

\begin{equation*} \int_{C(t)}\left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx =\int_0^1\left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\pd{\bx}{s}\de s. \end{equation*}

We use the identity

\begin{equation*} \left(\mathbf{p}\times\mathbf{q}\right)\times\mathbf{r} =\left(\mathbf{p}\cdot\mathbf{r}\right)\mathbf{q} -\left(\mathbf{q}\cdot\mathbf{r}\right)\mathbf{p}, \end{equation*}

and

\begin{equation*} \int_{C(t)}\left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx =\int_0^1\left(\pd{\mathbf{a}}{t}\cdot\pd{\bx}{s} +\left(\bu\cdot\nabla\mathbf{a}\right)\cdot\pd{\bx}{s} -\left(\pd{\bx}{s}\cdot\nabla\mathbf{a}\right)\cdot\bu\right)\de s. \end{equation*}

🔗

Hence,

\begin{align*} \dd{\mathcal{C}}{t} -\int_{C(t)}\left(\pd{\mathbf{a}}{t} +\left(\nabla\times\mathbf{a}\right)\times\bu\right)\cdot\de\bx =& \int_0^1\left(\mathbf{a}\cdot\pd{\bu}{s} +\left(\pd{\bx}{s}\cdot\nabla\mathbf{a}\right)\cdot\bu\right)\de s\\ =& \int_0^1\left(\mathbf{a}\cdot\pd{\bu}{s} +\pd{\mathbf{a}}{s}\cdot\bu\right)\de s\\ =& \int_0^1\pd{}{s}\left(\mathbf{a}\cdot\bu\right)\de s\\ =&0, \end{align*}

whence the result.

🔗

4. Axisymmetric flow.

Please feel free to omit this problem as we have not covered the material.

🔗

(Based on Exercise 5.7 in [4]). In this question, please make use of the vector calculus formulae given in cylindrical polar coordinates, available at this website. Consider an axisymmetric flow. Working in cylindrical polar coordinates \((r,\theta,z)\text{,}\) show that the vorticity is given by

\begin{equation*} \bomega=\omega\be_{\theta}, \end{equation*}

and that the vorticity equation (3.5.8) reduces to

\begin{equation*} \DD{}{t}\left(\frac{\omega}{r}\right)=0. \end{equation*}

Thus the vorticity changes in proportion to distance from the axis of symmetry.

🔗

Note that in spherical polar coordinates \((r,\theta,\phi)\) this is equivalent to

\begin{equation*} \bomega=\omega\be_{\phi},\quad \DD{}{t}\left(\frac{\omega}{r\sin\theta}\right)=0. \end{equation*}

🔗

Hint.

Axisymmetry implies that \(\bu\) has no \(\theta\)-component, that is \(\bu\cdot\be_{\theta}=0\text{,}\) and that \(\partial\bu/\partial\theta=0\text{.}\) Hence, \(\bu=(u_r(r,z,t),0,u_z(r,z,t))\text{.}\)

🔗

Then, using the formula for curl in cylindrical polar coordinates,

\begin{equation*} \bomega=\nabla\times\bu =\left(\pd{u_r}{z}-\pd{u_z}{r}\right)\be_{\theta}. \end{equation*}

🔗

We have

\begin{align*} &\DD{\bomega}{t}-\bomega\cdot\nabla\bu=0\\ \Rightarrow\quad&\DD{\omega}{t}\be_{\theta}+\omega\DD{\be_{\theta}}{t} -\omega\be_{\theta}\cdot\nabla\bu=0. \end{align*}

Show that \(\mathrm{D}\be_{\theta}/\mathrm{D}t=0\) and use

\begin{equation*} \pd{\bu}{\theta}=u_r\be_{\theta}. \end{equation*}

🔗

Solution.

🔗

Then, using the formula for curl in cylindrical polar coordinates,

\begin{equation*} \bomega=\nabla\times\bu =\left(\pd{u_r}{z}-\pd{u_z}{r}\right)\be_{\theta} =\omega\be_{\theta}, \end{equation*}

where \(\omega=\partial u_r/\partial z-\partial u_z/\partial r\text{.}\)

🔗

We have

\begin{align*} &\DD{\bomega}{t}-\bomega\cdot\nabla\bu=0\\ \Rightarrow\quad&\DD{\omega}{t}\be_{\theta}+\omega\DD{\be_{\theta}}{t} -\omega\be_{\theta}\cdot\nabla\bu=0. \end{align*}

We note that \(\partial\be_{\theta}/\partial t=0\) and \((\bu\cdot\nabla)\) has gradients with respect to \(r\) and \(z\) (and not with respect to \(\theta\)), meaning that \((\bu\cdot\nabla)\be_{\theta}=0\text{.}\) Also, since \(\partial\be_r/\partial\theta=\be_\theta\text{,}\)

\begin{equation*} \be_{\theta}\cdot\nabla\bu=\frac1r\pd{}{\theta}\left(u_r(r,z,t)\be_r+u_z(r,z,t)\be_z\right)=\frac{u_r}{r}\be_{\theta}. \end{equation*}

Hence, the only non-zero component of the vorticity equation is the \(\theta\)-component, and this reads:

\begin{equation*} \DD{\omega}{t}-\omega\frac{u_r}{r}=0. \end{equation*}

🔗

Now,

\begin{equation*} \DD{}{t}\left(\frac{\omega}{r}\right)=\frac1r\DD{\omega}{t}-\frac{\omega}{r^2}\DD{r}{t}, \end{equation*}

and

\begin{equation*} \DD{r}{t}=u_r\pd{r}{r}=u_r \end{equation*}

and hence

\begin{equation*} \DD{}{t}\left(\frac{\omega}{r}\right)=\frac1r\DD{\omega}{t}-\frac{\omega u_r}{r^2}. \end{equation*}

🔗

Dividing the vorticity equation by \(r\text{:}\)

\begin{equation*} \frac1r\DD{\omega}{t}-\frac1r\omega\frac{u_r}{r}=0 \quad\Rightarrow\quad \DD{}{t}\left(\frac{\omega}{r}\right)=0, \end{equation*}

as required.

🔗

5. Two vortices.

Two vortices, of strengths \(\Gamma_1\) and \(\Gamma_2\text{,}\) are at the points \(z = z_1\) and \(z = z_2\text{,}\) respectively, in the complex plane. Write down the equations of motion for the position vectors \(z_1(t)\) and \(z_2(t)\) if the vortices are free to move. Assuming that \(\Gamma_1+\Gamma_2\neq0\text{,}\) show that \(\de Z/\de t = \de a/\de t = 0\text{,}\) where

\begin{equation*} Z=\frac{\Gamma_1z_1+\Gamma_2z_2}{\Gamma_1+\Gamma_2} \end{equation*}

is the centroid of the two vortices, and \(a = |z_1− z_2|\) is the distance between them.

🔗

Deduce that each vortex moves in a circle centred on \(Z\text{,}\) with angular velocity

\begin{equation*} \Omega=\frac{\Gamma_1+\Gamma_2}{2\pi a^2}. \end{equation*}

What happens in the exceptional case where \(\Gamma_1+\Gamma_2=0\text{?}\)

🔗

Hint.

The complex potential for the two vortices is

\begin{equation*} w(z)=-\frac{\im\Gamma_1}{2\pi}\log(z-z_1)-\frac{\im\Gamma_2}{2\pi}\log(z-z_2). \end{equation*}

Hence, the velocity field is given by

\begin{equation*} u-\im v=-\frac{\im\Gamma_1}{2\pi(z-z_1)}-\frac{\im\Gamma_2}{2\pi(z-z_2)}. \end{equation*}

The velocity of each vortex is given by evaluating this expression at the position of the other vortex.

🔗

Solution.

The complex potential for the two vortices is

\begin{equation*} w(z)=-\frac{\im\Gamma_1}{2\pi}\log(z-z_1)-\frac{\im\Gamma_2}{2\pi}\log(z-z_2). \end{equation*}

Hence, the velocity field is given by

\begin{equation*} u-\im v=-\frac{\im\Gamma_1}{2\pi(z-z_1)}-\frac{\im\Gamma_2}{2\pi(z-z_2)}. \end{equation*}

The velocity of each vortex is given by evaluating this expression at the position of the other vortex.

🔗

Thus, the equations of motion for the vortices are

\begin{align*} \dd{z_1}{t}=&-\frac{\im\Gamma_2}{2\pi(z_1-z_2)},\\ \dd{z_2}{t}=&-\frac{\im\Gamma_1}{2\pi(z_2-z_1)}. \end{align*}

🔗

We calculate

\begin{align*} \dd{Z}{t}=&\frac{\Gamma_1}{\Gamma_1+\Gamma_2}\dd{z_1}{t} +\frac{\Gamma_2}{\Gamma_1+\Gamma_2}\dd{z_2}{t}\\ =&-\frac{\im\Gamma_1\Gamma_2}{2\pi(\Gamma_1+\Gamma_2)} \left(\frac1{z_1-z_2}-\frac1{z_2-z_1}\right)\\ =&0. \end{align*}

Similarly,

\begin{align*} \dd{a^2}{t}=&\dd{}{t}\left((z_1-z_2)(\overline{z_1-z_2})\right)\\ =&(z_1-z_2)\dd{}t(\overline{z_1-z_2}) +(\overline{z_1-z_2})\dd{}{t}(z_1-z_2)\\ =&(z_1-z_2)\left(\overline{\dd{z_1}{t}}-\overline{\dd{z_2}{t}}\right) +(\overline{z_1-z_2})\left(\dd{z_1}{t}-\dd{z_2}{t}\right)\\ =&\frac{\im\Gamma_1\Gamma_2}{2\pi} \left(\frac{z_1-z_2}{\overline{z_1-z_2}} -\frac{\overline{z_1-z_2}}{z_1-z_2}\right)\\ =&0. \end{align*}

🔗

Thus, \(Z\) and \(a\) are constant in time. To find the angular velocity, we set \(z_1=Z+a\exp(\im\theta_1)\)

🔗

6. Obstacle.

Fluid occupies the region \(x^2+y^2>a^2\) outside a circular obstacle of radius \(a\text{.}\) By using the Milne-Thomson Circle Theorem, find the resulting complex potential when a vortex of strength \(\Gamma\) is placed at \((x, y) = (b, 0)\text{,}\) where \(b > a\) (assuming there to be no circulation about the obstacle).

🔗

Explain why the vortex will move in a circle of radius \(b\) with angular velocity of magnitude

\begin{equation*} \Omega=\frac{\Gamma a^2}{2\pi b^2(b^2-a^2)}. \end{equation*}

🔗

Hint.

The complex potential associated with a vortex in isolation at the point \(c\) is

\begin{equation*} f(z)=-\frac{\im\Gamma}{2\pi}\log(z-c). \end{equation*}

The Milne-Thomson Circle Theorem Theorem 4.6.1 states that, for a complex potential \(g(z)\text{,}\) the function

\begin{equation*} w(z)=g(z)+\overline{g\left(\frac{R^2}{\overline{z}}\right)} \end{equation*}

has the same singularities as \(g(z)\) outside the circle \(|z|=R\) and that \(|z|=R\) is a streamline of the flow with complex potential \(w(z)\text{.}\) Removing the line vortex from the associated flow allows its velocity to be found.

🔗

Solution.

The complex potential associated with the vortex in isolation is

\begin{equation*} f(z)=-\frac{\im\Gamma}{2\pi}\log(z-b). \end{equation*}

We construct the complex potential in the presence of the obstacle using the Milne-Thomson Circle Theorem:

\begin{align*} w(z)=&f(z)+\overline{f\left(\frac{a^2}{\overline{z}}\right)}\\ =&-\frac{\im\Gamma}{2\pi}\log(z-b) +\frac{\im\Gamma}{2\pi}\overline{\log\left(\frac{a^2}{\overline{z}}-b\right)}\\ =&-\frac{\im\Gamma}{2\pi}\log(z-b) +\frac{\im\Gamma}{2\pi}\log\left(\frac{a^2}{z}-b\right)\\ =&\frac{\im\Gamma}{2\pi}\log\left(\frac{a^2-bz}{z(z-b)}\right)\\ =&\frac{\im\Gamma}{2\pi}\left(\log\left(a^2-bz\right)-\log z-\log(z-b)\right); \end{align*}

separating the logarithms in the final step enables the derivative to be taken more easily. This has a single singularity at the vortex \(z=b\) and the circle \(|z|=a\) is a streamline, as required.

🔗

The velocity field can be found by taking the derivative of \(w(z)\text{:}\)

\begin{align*} u-\im v&=\dd{w}{z}\\ =&-\frac{\im\Gamma}{2\pi}\left(\frac{b}{a^2-bz}+\frac1{z-b}+\frac1{z}\right), \end{align*}

and, removing the vortex (the term proportional to \(1/(z-b)\)), the velocity of the vortex at \(z=b\) is

\begin{equation*} u_V-\im v_V=-\frac{\im\Gamma}{2\pi}\left(\frac{b}{a^2-b^2}+\frac1{b}\right), \end{equation*}

which is an instantaneous velocity of magnitude

\begin{equation*} \frac{\Gamma}{2\pi}\left(\frac{b}{a^2-b^2}+\frac1{b}\right) \end{equation*}

upwards. By symmetry, the vortex moves in a circle of radius \(b\) about the origin with speed equal to this value, giving an angular velocity of

\begin{equation*} \frac{\Gamma}{2\pi}\left(\frac1{a^2-b^2}+\frac1{b^2}\right) =\frac{\Gamma a^2}{2\pi b^2(a^2-b^2)}. \end{equation*}

This is negative, so the line vortex goes clockwise around the origin with angular velocity

\begin{equation*} \frac{\Gamma a^2}{2\pi b^2(b^2-a^2)}. \end{equation*}

as required.

🔗

7. Flow in a quadrant.

Fluid occupies the quadrant \(x > 0\text{,}\) \(y > 0\) bounded by two rigid boundaries along the \(x\)- and \(y\)-axes. Find the complex potential for the flow caused by a vortex at a point \(z=c=a+\im b\) in the fluid. If the vortex is free to move, show that it follows a path on which

\begin{equation*} \frac1{x^2}+\frac1{y^2}=\text{constant}. \end{equation*}

🔗

Solution.

See also Example 6.2.16.

🔗

Suppose the vortex is at the point

\begin{equation*} z_1=x_1+\im y_1. \end{equation*}

We use three image vortices at \(x_1-\im y_1\) and at \(-x_1+\im y_1\text{,}\) both of strength \(-\Gamma\text{,}\) and at \(-x_1-\im y_1\) of strength \(\Gamma\text{.}\)

🔗

Recall that the complex potential of a line vortex at \(z=c\) of strength \(\Gamma\) is \(-\im\Gamma\log(z-c)/(2\pi)\) and its velocity is given by the derivative of this map: \(u-\im v=-\im\Gamma/(2\pi(z-c))\text{.}\)

🔗

The velocity of the vortex is given by the sum of the velocities due to the other three vortices:

\begin{align*} \dd{x_1}{t}-\im\dd{y_1}{t} =&\frac{\im\Gamma}{2\pi((x_1+\im y_1)-(x_1-\im y_1))}\\ &+\frac{\im\Gamma}{2\pi((x_1+\im y_1)-(-x_1+\im y_1))}\\ &-\frac{\im\Gamma}{2\pi((x_1+\im y_1)-(-x_1-\im y_1))}\\ &=\frac{\im\Gamma}{4\pi}\left(\frac1{x_1}+\frac1{\im y_1}-\frac1{x_1+\im y_1}\right). \end{align*}

Hence

\begin{gather*} \dd{x_1}{t} =\frac{\Gamma}{4\pi}\left(\frac1{y_1}-\frac{y_1}{x_1^2+y_1^2}\right) =\frac{\Gamma x_1^2}{4\pi y_1(x_1^2+y_1^2)},\\ \dd{y_1}{t} =\frac{\Gamma}{4\pi}\left(-\frac1{x_1}+\frac{x_1}{x_1^2+y_1^2}\right) =-\frac{\Gamma y_1^2}{4\pi x_1(x_1^2+y_1^2)}, \end{gather*}

and therefore

\begin{equation*} \dd{y_1}{x_1}=-\frac{y_1^3}{x_1^3}, \end{equation*}

which can be solved by separation of variables to give

\begin{equation*} \int\frac1{y_1^3}\de y_1=-\int\frac1{x_1^3}\de x_1 \quad\Rightarrow\quad -\frac1{2y_1^2}=\frac1{2x_1^2}+c, \end{equation*}

where \(c\) is constant, and this can be rearranged into the required form.

🔗

8. Channel flow.

[Harder] Fluid occupies the semi-infinite channel \(\{z : \Re z > 0,−a < \Im z < a\}\text{.}\) Show that the flow induced by a line vortex of strength \(\Gamma>0\) at the point \(z = d \in\mathbb{R}^+\) has complex potential

\begin{align*} w(z)=&\frac{\im\Gamma}{2\pi}\left\{ -\log\left[\sinh\left(\frac{\pi z}{2a}\right) -\sinh\left(\frac{\pi d}{2a}\right)\right]\right.\\ &+\left. \log\left[\sinh\left(\frac{\pi z}{2a}\right) +\sinh\left(\frac{\pi d}{2a}\right)\right] \right\}. \end{align*}

Show that the velocity components satisfy

\begin{equation*} u-\im v=\frac{\im\Gamma}{4a}\left\{ \mathrm{cosech}\left(\frac{\pi(z+d)}{2a}\right) -\mathrm{cosech}\left(\frac{\pi(z-d)}{2a}\right) \right\}. \end{equation*}

🔗

Deduce that, if the vortex is free to move, it will instantaneously travel downwards with speed \((\Gamma/4a)\mathrm{cosech}(\pi d/a)\text{.}\)

🔗

You may use the identities

\begin{equation*} \sinh^2(x)− \sinh^2(y) \equiv \sinh(x + y) \sinh(x− y) \end{equation*}

and

\begin{equation*} \cosh x\sinh y=\frac12\left(\sinh(x+y)+\sinh(y-x)\right). \end{equation*}

🔗

Hint.

Consider the map

\begin{equation*} \zeta = \sinh\left(\frac{\pi z}{2a}\right). \end{equation*}

🔗

Solution.

Consider the transformation

\begin{align*} \zeta =& \sinh\left(\frac{\pi z}{2a}\right)\\ =& \sinh\left(\frac{\pi (x+\im y)}{2a}\right)\\ =& \sinh\left(\frac{\pi x}{2a}\right)\cosh\left(\frac{\im\pi y}{2a}\right)+\cosh\left(\frac{\pi x}{2a}\right)\sinh\left(\frac{\im\pi y}{2a}\right)\\ =& \sinh\left(\frac{\pi x}{2a}\right)\cos\left(\frac{\pi y}{2a}\right)+\im\cosh\left(\frac{\pi x}{2a}\right)\sin\left(\frac{\pi y}{2a}\right). \end{align*}

The inverse transformation is

\begin{equation*} z = \frac{2a}{\pi}\sinh^{-1}\left(\zeta\right). \end{equation*}

🔗

With this map, the line \(x=0\) transforms to part of the imaginary axis

\begin{equation*} \zeta=\im\sin\left(\frac{\pi y}{2a}\right), \end{equation*}

and the constraint \(-a\lt y\lt a\) corresponds to the line between the points \(\pm\im\text{.}\) The lines \(y=\pm a\) transform to

\begin{equation*} \zeta=\pm\im\cosh\left(\frac{\pi x}{2a}\right), \end{equation*}

and the constraint \(x>0\) corresponds to the line segments above \(+\im\) and below \(-\im\text{,}\) respectively. Hence the channel is transformed to the right half plane:

🔗

Channel map — Figure 6.5.4. Conformal map of channel
🔗

We have a vortex of strength \(\Gamma\) at the point \(z=d\text{,}\) which point transforms to \(\zeta=\sinh(\pi d/(2a))\text{.}\) In the \(\zeta\)-plane, we also require an image vortex of strength \(-\Gamma\) at the point \(\zeta=-\sinh(\pi d/(2a))\text{.}\) This will ensure that the transformed channel boundary in the \(\zeta\)-plane (i.e. the imaginary axis) has a no-penetration boundary condition.

🔗

Therefore, the complex potential in the \(\zeta\)-plane is given by

\begin{equation*} g(\zeta) = -\frac{\im\Gamma}{2\pi}\log\left(\zeta-\sinh\left(\frac{\pi d}{2a}\right)\right) +\frac{\im\Gamma}{2\pi}\log\left(\zeta+\sinh\left(\frac{\pi d}{2a}\right)\right) \end{equation*}

Hence in the \(z\)-plane, the map is

\begin{align*} f(z) = & -\frac{\im\Gamma}{2\pi}\log\left(\sinh\left(\frac{\pi z}{2a}\right) -\sinh\left(\frac{\pi d}{2a}\right)\right)\\ & +\frac{\im\Gamma}{2\pi}\log\left(\sinh\left(\frac{\pi z}{2a}\right)+\sinh\left(\frac{\pi d}{2a}\right)\right)\\ = & \frac{\im\Gamma}{2\pi}\log\left(\frac{\sinh(\pi z/(2a))+\sinh(\pi d/(2a))}{\sinh(\pi z/(2a))-\sinh(\pi d/(2a))}\right) \end{align*}

🔗

The velocity components are given by the derivative:

\begin{align*} u-\im v = & f’(z)\\ = & \frac{\im\Gamma}{4a}\left( -\frac{\cosh(\pi z/(2a))}{\sinh(\pi z/(2a))-\sinh(\pi d/(2a))}\right.\\ & \left.+\frac{\cosh(\pi z/(2a))}{\sinh(\pi z/(2a))+\sinh(\pi d/(2a))} \right)\\ = & -\frac{\im\Gamma}{2a}\left( \frac{\cosh(\pi z/(2a))\sinh(\pi d/(2a))}{\sinh^2(\pi z/(2a))-\sinh^2(\pi d/(2a))} \right) \end{align*}

Using the identity given in the question, we have,

\begin{align*} f’(z)=& -\frac{\im\Gamma}{2a}\left( \frac{\cosh(\pi z/(2a))\sinh(\pi d/(2a))}{\sinh(\pi(z+d)/(2a))\sinh(\pi(z-d)/(2a))} \right)\\ =& -\frac{\im\Gamma}{4a}\left( \frac{\sinh(\pi(d+z)/(2a))+\sinh(\pi(d-z)/(2a))}{\sinh(\pi(z+d)/(2a))\sinh(\pi(z-d)/(2a))} \right)\\ =& -\frac{\im\Gamma}{4a}\left( \mathrm{cosech}\left(\frac{\pi(z-d)}{2a}\right) -\mathrm{cosech}\left(\frac{\pi(z+d)}{2a}\right) \right), \end{align*}

as required.

🔗

Using the Helmholtz principle, the vortex moves due to the flow of everything but itself. Thus at \(z=d\text{,}\) excluding the part of the flow due to the vortex, if the vortex flow moves with velocity \((u_V,v_V)\text{,}\) we have

\begin{equation*} u_V-\im v_V =-\frac{\im\Gamma}{4a}\mathrm{cosech}\left(\frac{\pi d}{a}\right), \end{equation*}

corresponding to a downward velocity

\begin{equation*} \frac{\Gamma}{4a}\mathrm{cosech}\left(\frac{\pi d}{a}\right). \end{equation*}

🔗

Prev Top Next