Exercises

Exercises 3.6 Exercises

This chapter focused on deriving the key Euler equations for an inviscid and incompressible flow, starting from first principles, and deriving the conservation laws using vector calculus. Eventually, we studied different variations of the Euler equations and its consequences.

🔗

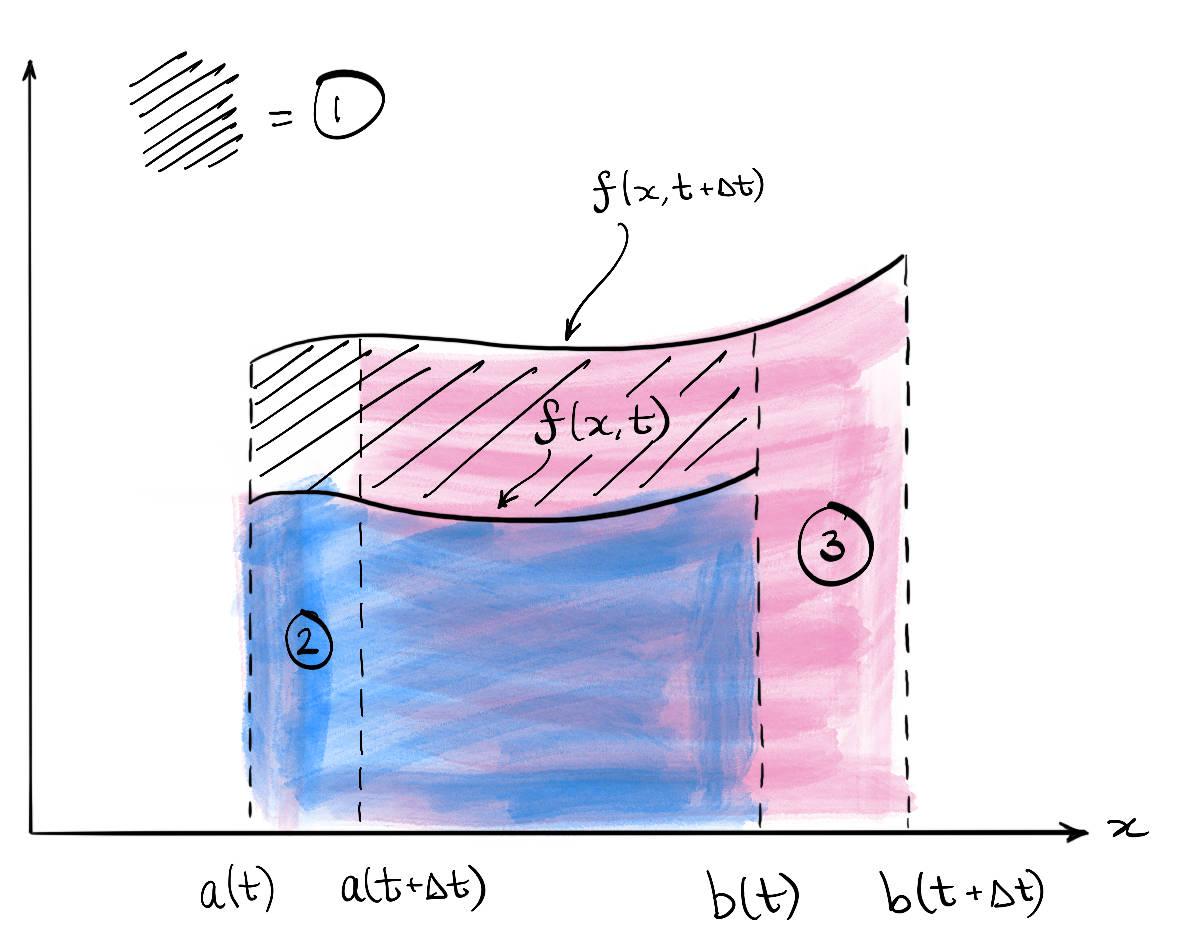
1. Continuum approximation.

Domestic salt flows quite well out of a container with a hole in the bottom. Following Remark 3.0.3, consider whether salt matches up to the properties quoted for a fluid

🔗

What is the size of a typical salt particle? What size of hole would required so that a continuum model of the salt flow is a reasonable assumption? (Based on Q1, p. 42 by Paterson [10].)

🔗

Solution.

Salt is not like a fluid because you can make it into a pile, whereas the surface of a resting fluid is always horizontal. However, some aspects of salt flow are similar to the flow of a fluid. A typical salt particle is approximately a cube of side \(0.5\) mm, and therefore has a volume of approximately \(10^{-10}\) m\(^3\text{.}\) We need a size of hole that admits a very large number of particles. A reasonable value of the volume \(V\) appearing in the continuum approximation might be the volume of \(3\times10^7\) salt grains (this was the number of gas or liquid molecules quoted in the notes), i.e. \(3\times10^{-3}\) m\(^3\text{,}\) which is a cube of side length approximately \(10\) cm. We need a hole that is many times this distance, perhaps a hole with a diameter of one metre or so might be reasonable! See also Remark 3.0.3.

🔗

2. Bump lemma.

Within our derivations of the governing equations, we often make use of the so-called "Bump lemma" given in Lemma 3.2.2.

🔗

Give a proof of the lemma.

🔗

Solution.

This proof assumes that the function \(f\) is not pathological (e.g. it cannot oscillate infinitely fast, take different values for rational vs. irrational, etc.). That’s what we mean by "sufficiently smooth".

🔗

Assume that there exists a point \(\bx_0 \in \Omega\) where \(f(\bx_0) \neq 0\text{.}\) Suppose without loss of generality \(f > 0\) here. Since \(f\) is sufficiently smooth (and in particular, it is continuous), then there exists a non-trivial neighbourhood near \(\bx_0\) where \(f > 0\) everywhere in this neighbourhood, say \(V_0\text{.}\) Then \(\int_{V_0} f \, \de{V} = 0\text{,}\) contradicting the assumption. Therefore \(f\) must be zero everywhere.

🔗

3. Leibnitz’s rule.

The Reynolds’ Transport Theorem Theorem 3.1.3, which relates to the passage of a time derivative through an integral, is a general form of the 1D Leibnitz rule:

\begin{align} \dd{}{t} & \int_{a(t)}^{b(t)} f(x, t) \, \de{x} \notag\\ & = \int_{a(t)}^{b(t)} \pd{f}{t} \, \de{x} + f(b(t), t) \dot{b}(t) - f(a(t), t)\dot{a}(t).\tag{3.6.1} \end{align}

🔗

(a)

Examine the figure in Figure 3.6.1. Can you associate the quantities in Leibnitz’s rule with the circled elements in the figure?

🔗

Solution.

The first circled element is associated with the quantity:

\begin{equation*} \frac{1}{\Delta t} \int_{a(t)}^{b(t)} [f(x, t + \Delta t) - f(x, t)] \, \de{x}. \end{equation*}

This is essentially the finite-difference version of the first term on the RHS.

🔗

The second circled element is associated with the quantity:

\begin{equation*} f(x, t)[a(t + \Delta t) - a(t)] \frac{1}{\Delta t}, \end{equation*}

and is associated with the area of the rectangle.

🔗

The third circled element is associated with

\begin{equation*} f(x, t + \Delta t)[b(t + \Delta t) - b(t)] \frac{1}{\Delta t}, \end{equation*}

and is associated with the area of the rectangle. Notice that for small \(\Delta t\text{,}\) the rectangle height of \(f(x, t+\Delta t)\) is approximately the same as the rectangle height of \(f(x, t)\text{.}\)

🔗

(b)

A nice proof of the Leibnitz rule is given in this YouTube video by Brian Storey. Watch the video and follow the derivation, making your own notes.

🔗

(c)

Can you now connect the form of the rule in (3.6.1) to the Reynolds’ Transport Theorem in (3.1.2)?

🔗

Solution.

Show that the Reynolds Transport Theorem in one dimension is equivalent to the Leibniz rule. Write the second and third terms on the RHS as

\begin{equation*} \int_{a(t)}^{b(t)} \dd{}{x}(f(x, t) u(x, t)) \, \de{x}. \end{equation*}

🔗

4. Derivation of governing equations.

This is a re-derivation of what is already presented in the notes, giving you valuable practice to understand the concepts.

🔗

Starting from conservation of mass and momentum for a material volume moving in an inviscid fluid, use Reynolds’ Transport Theorem (3.1.2) to derive the equations:

\begin{gather} \pd{\rho}{t} + \nabla \cdot(\rho \bu) = 0, \tag{3.6.2}\\ \DD{\bu}{t} = -\frac{1}{\rho} \nabla p + \bg. \tag{3.6.3} \end{gather}

🔗

What additional assumptions are required to transform the set of equations to the Euler equations of Definition 3.4.5? Apply these assumptions and conclude with the Euler equations.

🔗

Solution.

The proof of the continuity equation is given in Theorem 3.2.1 and the proof of the momentum equation is given in Theorem 3.3.1, so make sure you can follow these arguments and produce your own notes.

🔗

The derivation of the Euler equations, as given in Definition 3.4.5 requires the additional assumption of an incompressible fluid, following Theorem 3.4.1. Incompressibility implies that \(\nabla \cdot \bu = 0\text{,}\) and this equation then replaces the continuity equation.

🔗

5. Pressure field in uniform flow.

An ideal (incompressible and irrotational) fluid in a gravitational field with density \(\rho\) and acceleration vector \(\bg = -g \bk\) (with \(\bk\) being the unit vector in the positive \(z\)-direction) has uniform velocity

\begin{equation*} \bu = (a + b t, \; t^3, \; e^t). \end{equation*}

The pressure at the origin is fixed at \(p_0\text{.}\)

🔗

(a)

Using the Euler equations in Definition 3.4.5, find the pressure field in terms of \(x, y, z, t, a, b, g, \rho\) and \(p_0\text{.}\)

🔗

Solution.

The fluid has a uniform velocity, which means that all components of \(\nabla\bu\) vanish. The Euler equation simplifies to

\begin{equation*} \rho\pd{\bu}{t}=-\nabla p-\rho g \bk, \end{equation*}

where

\begin{equation*} \pd{\bu}{t}=(b, \; 3t^2, \; e^t). \end{equation*}

Hence, the pressure is given by solving the equation,

\begin{equation*} \nabla p = -\rho \pd{\bu}{t} - \rho g \bk = -\rho (\, b, \; 3t^2, \; e^t + g \,), \end{equation*}

which is a vector equation. Splitting into components, we obtain

\begin{equation*} \frac{\partial p}{\partial x} = -\rho b, \quad \frac{\partial p}{\partial y} = -3\rho t^2, \quad \frac{\partial p}{\partial z} = -\rho (e^t + g). \end{equation*}

Solving sequentially, the first equation gives

\begin{equation*} p = -\rho b x + f_1(y,z,t). \end{equation*}

Substituting into the second equation,

\begin{equation*} \frac{\partial f_1}{\partial y} = -3\rho t^2 \;\;\Rightarrow\;\; f_1 = -3\rho t^2 y + f_2(z,t), \end{equation*}

\begin{equation*} p = -\rho b x - 3\rho t^2 y + f_2(z,t). \end{equation*}

The third equation then implies

\begin{equation*} \frac{\partial f_2}{\partial z} = -\rho(e^t+g) \;\;\Rightarrow\;\; f_2 = -\rho(e^t+g)z + f_3(t), \end{equation*}

\begin{equation*} p = -\rho b x - 3\rho t^2 y - \rho(e^t+g)z + f_3(t). \end{equation*}

Using \(p = p_0\) at the origin gives \(f_3(t) = p_0\) for all \(t\text{.}\) Hence

\begin{equation*} p = p_0 - \rho \big(bx + 3t^2 y + (e^t + g)z \big). \end{equation*}

🔗

(b)

What can you tell about the surfaces of constant pressure? Sketch this at a fixed time \(t\text{,}\) and hence describe the pressure field.

🔗

Solution.

The pressure is constant on parallel planes normal to the vector \((b, \; 3t^2, \; e^t + g)\text{,}\) as illustrated below:

🔗

Figure 3.6.2. Contours of the pressure field at fixed \(t\text{.}\)
🔗

🔗

6. Piston problem.

The piston shown in the diagram below is pushed with a force \(F(t)\) into a pipe of length \(L\) and cross-sectional area \(A\) containing incompressible and irrotational fluid of density \(\rho\text{.}\)

🔗

Figure 3.6.3. Schematic of piston and pipe system.
🔗

Assume that the pressure at the open end is held at atmospheric pressure, \(p = p_\text{atm}\text{.}\)

🔗

Assume the fluid moves as a rigid body and neglect friction and the mass of the piston. Using the Euler equations in Definition 3.4.5, write down a differential equation governing the position, \(X(t)\text{,}\) of the piston at time \(t\text{.}\) You may neglect gravity. You do not need to solve the equation (it could be solved using Python or similar).

🔗

Solution.

We assume that the fluid pressure at the open end of the pipe is atmospheric pressure. Since the fluid moves as a rigid body, the velocity field has no spatial gradients, and hence the Euler equation reduces to

\begin{equation*} \rho\pd{\bu}{t}=-\nabla p, \end{equation*}

where the velocity is uniformly \(\bu=(\dot{X}(t),0)\text{.}\)

🔗

Solving for \(p\) and using the fact that \(p\) is atmospheric pressure at \(x = L\text{,}\) we have

\begin{equation*} p(x,t) = \rho\dd{^2 X}{t^2}(L-x)+p_\text{atm}. \end{equation*}

🔗

At the piston \(x=X\text{,}\) note that atmospheric pressure applies in addition to \(F\text{,}\) meaning that the force on the fluid is

\begin{equation*} F+Ap_\text{atm}, \end{equation*}

and hence the fluid pressure is

\begin{equation*} \frac{F}{A} + p_\text{atm}. \end{equation*}

Then

\begin{equation*} \frac{F}{A} + p_\text{atm} = \rho\dd{^2X}{t^2}(L-X)+p_\text{atm} \quad\Rightarrow\quad \dd{^2X}{t^2} = \frac{F}{A\rho(L-X)}. \end{equation*}

🔗

Note that the atmospheric pressure cancels in this problem, and this is common to problems of this type, because atmospheric pressure acts uniformly on all surfaces exposed to the atmosphere and therefore does not lead to a resultant force or affect the dynamics. This motivates the introduction of a gauge pressure, \(p_{\text{gauge}}\text{,}\) whereby a uniform and constant baseline pressure is chosen, in this case \(p_{\text{atm}}\text{,}\) with the gauge pressure given by \(p_{\text{gauge}}=p-p_{\text{atm}}\text{.}\) Since the pressure only appears as a gradient in the governing equations, using the gauge pressure does not affect the result. Introducing a gauge pressure can make the algebra simpler.

🔗

7. The vorticity equation.

Consider an incompressible fluid, with constant density \(\rho\text{,}\) subject to a conservative body force (i.e. \({\bg} = -\nabla \chi\) for some potential function \(\chi\)).

🔗

(a)

Starting from the Euler equations, show that the vorticity \(\bomega = \nabla \times {\bu}\) satisfies

\begin{equation*} \frac{D \bomega}{Dt} = (\bomega \cdot \nabla){\bu}. \end{equation*}

Note that, in this question, you are expected to do a long-form calculation. The method given in the notes uses an alternative expression for the momentum equation combined with a vector identity to get the same result with less effort.

🔗

Solution.

The Euler equation reads:

\begin{equation*} \rho\left(\pd{\bu}{t} + (\bu \cdot \nabla)\bu\right) = -\nabla p - \rho\nabla \chi. \end{equation*}

Since the curl of a gradient is zero, \(\rho\) is constant and we can commute derivatives, taking the curl of both sides gives

\begin{equation*} \rho\left(\pd{\bomega}{t} + \nabla \times(\bu \cdot \nabla)\bu\right) = 0. \end{equation*}

We have

\begin{align*} & \nabla \times(\bu \cdot \nabla)\bu,\\ =&\begin{vmatrix} \bi & \bj & \bk \\ \pd{}{x} & \pd{}{y} & \pd{}{z} \\ \bu \cdot \nabla u & \bu \cdot \nabla v & \bu \cdot \nabla w \end{vmatrix},\\ =&\bi\left(\bu\cdot\nabla\left(\pd{w}{y}-\pd{v}{z}\right)+\pd{\bu}{y}\cdot\nabla w-\pd{\bu}{z}\cdot\nabla v\right)\\ &+\bj\left(\bu\cdot\nabla\left(\pd{u}{z}-\pd{w}{x}\right)+\pd{\bu}{z}\cdot\nabla u-\pd{\bu}{x}\cdot\nabla w\right)\\ &+\bk\left(\bu\cdot\nabla\left(\pd{v}{x}-\pd{u}{y}\right)+\pd{\bu}{x}\cdot\nabla v-\pd{\bu}{y}\cdot\nabla u\right), \end{align*}

At this point, note that we can see \(\bu\cdot\nabla\bomega\) appearing in the components, but it is not so easy to see how to make out the terms of \(\bomega\cdot\nabla\bu\text{.}\) Since we know what we are aiming for, we instead calculate

\begin{align*} & \nabla \times(\bu \cdot \nabla)\bu -\left(\bu\cdot\nabla\bomega-\bomega\cdot\nabla\bu\right)\\ =&\bomega\cdot\nabla\bu\\ &+\bi\left(\pd{u}{y}\pd{w}{x}+\pd{v}{y}\pd{w}{y}+\pd{w}{y}\pd{w}{z}-\pd{u}{z}\pd{v}{x}-\pd{v}{z}\pd{v}{y}-\pd{w}{z}\pd{v}{z}\right)\\ &+\bj\left(\pd{u}{z}\pd{u}{x}+\pd{v}{z}\pd{u}{y}+\pd{w}{z}\pd{u}{z}-\pd{u}{x}\pd{w}{x}-\pd{v}{x}\pd{w}{y}-\pd{w}{x}\pd{w}{z}\right)\\ &+\bk\left(\pd{u}{x}\pd{v}{x}+\pd{v}{x}\pd{v}{y}+\pd{w}{x}\pd{v}{z}-\pd{u}{y}\pd{u}{x}-\pd{v}{y}\pd{u}{y}-\pd{w}{y}\pd{u}{z}\right),\\ =&\bi\left(\left(\pd{w}{y}-\pd{v}{z}\right)\pd{u}{x}+\left(\pd{u}{z}-\pd{w}{x}\right)\pd{u}{y}+\left(\pd{v}{x}-\pd{u}{y}\right)\pd{u}{z}\right)\\ &+\bj\left(\left(\pd{w}{y}-\pd{v}{z}\right)\pd{v}{x}+\left(\pd{u}{z}-\pd{w}{x}\right)\pd{v}{y}+\left(\pd{v}{x}-\pd{u}{y}\right)\pd{v}{z}\right)\\ &+\bk\left(\left(\pd{w}{y}-\pd{v}{z}\right)\pd{w}{x}+\left(\pd{u}{z}-\pd{w}{x}\right)\pd{w}{y}+\left(\pd{v}{x}-\pd{u}{y}\right)\pd{w}{z}\right)\\ &+\bi\left(\pd{u}{y}\pd{w}{x}+\pd{v}{y}\pd{w}{y}+\pd{w}{y}\pd{w}{z}-\pd{u}{z}\pd{v}{x}-\pd{v}{z}\pd{v}{y}-\pd{w}{z}\pd{v}{z}\right)\\ &+\bj\left(\pd{u}{z}\pd{u}{x}+\pd{v}{z}\pd{u}{y}+\pd{w}{z}\pd{u}{z}-\pd{u}{x}\pd{w}{x}-\pd{v}{x}\pd{w}{y}-\pd{w}{x}\pd{w}{z}\right)\\ &+\bk\left(\pd{u}{x}\pd{v}{x}+\pd{v}{x}\pd{v}{y}+\pd{w}{x}\pd{v}{z}-\pd{u}{y}\pd{u}{x}-\pd{v}{y}\pd{u}{y}-\pd{w}{y}\pd{u}{z}\right),\\ =&\bomega\nabla\cdot\bu,\\ =&0, \end{align*}

where the final equality follows from incompressibility. Hence,

\begin{equation*} \pd{\bomega}{t} + \bu\cdot\nabla\bomega - \bomega\cdot\nabla\bu = 0 \quad\Rightarrow\quad \DD{\bomega}{t} = (\bomega \cdot \nabla)\bu, \end{equation*}

as required.

🔗

(b)

Deduce that, in two-dimensional incompressible flow, \(\omega\) is conserved following the flow.

🔗

Solution.

If the flow is the \((x,y)\)-plane, we have \(w=0\) and all \(z\)-derivatives are zero. Hence the only non-zero component of the vorticity is the \(z\)-component, \(\omega_z=\partial v/\partial x-\partial u/\partial y\text{.}\) Thus

\begin{equation*} \bomega\cdot\nabla\bu=\omega_z\pd{\bu}{z}=0. \end{equation*}

Hence

\begin{equation*} \DD{\bomega}{t} = 0, \end{equation*}

meaning that \(\bomega\) is conserved following the flow.

🔗

8. Using streamlines: The clepsydra.

One of the earliest means for measuring the passage of time, invented by the ancient Egyptians, was the clepsydra (or ‘water thief’): a large jar with a hole in its base is filled with water. The shape of the jar was such that the interval of time taken for the water surface to pass two equally-spaced markers on the side of the jar is constant.

🔗

In this question you will determine the shape of jar required to achieve this. In particular, we denote the (axisymmetric) jar radius a height \(z\) above the hole by \(r = a(z)\text{.}\) The radius of the hole, \(a_h \ne a(0)\text{,}\) in general.

🔗

(a)

Explain why the curve \(r = a(z)\) is a streamline.

🔗

Solution.

The fluid velocity at the surface of the jar satisfies \(\bu\cdot\bn=0\text{,}\) so that no fluid leaves or enters the jar through its sides. This means that the flow next to the boundary of the jar must be parallel to this boundary, meaning that streamlines are parallel to the boundary. Equivalently, the boundary \(r = a(z)\) is a streamline.

🔗

(b)

If the surface of the water lies at \(z = h(t)\text{,}\) use an appropriate form of Bernoulli’s principle to calculate the speed of liquid, \(u\text{,}\) leaving the jar at \(z = 0\text{.}\)

🔗

[You may assume that the desired surface speed \(u_S = |\dot{h}| \ll u\text{,}\) so that the flow is approximately steady and that the fluid pressure is atmospheric at \(z = 0\) .]

🔗

Solution.

We apply Bernoulli’s equation to equate the energy at a point at the edge of the free surface at \(z = h(t)\) and the fluid leaving the hole at \(z = 0\text{.}\) At the free surface, the pressure is atmospheric, \(p = p_{atm}\text{,}\) and the speed is \(u_S\sqrt{1+a^{'2}}\text{.}\) At the hole, the pressure is also atmospheric, \(p = p_{atm}\text{,}\) and the velocity is \(u\text{.}\) Thus, Bernoulli’s equation for the streamline joining the two points gives

\begin{equation*} \frac{p_{atm}}{\rho} + \frac12 u_S^2(1+a^{'2}) + gh = \frac{p_{atm}}{\rho} + \frac12 u^2. \end{equation*}

Assuming that \(u_S \ll u\text{,}\) this simplifies to

\begin{equation*} gh = \frac12 u^2. \end{equation*}

🔗

(c)

Use the principle of conservation of mass to link \(u_S\text{,}\) \(u\text{,}\) \(a_h\) and \(a(h(t))\text{;}\) thereby determine the correct shape for a clepsydra.

🔗

Solution.

The volume flux out of the hole is \(\pi a_h^2 u\text{,}\) while the rate of decrease of the volume of fluid in the jar is \(\pi a(h(t))^2 u_S\text{.}\) Conservation of mass therefore gives

\begin{equation*} \pi a^2 u_S = \pi a_h^2 u, \end{equation*}

\begin{equation*} u_S = \frac{a_h^2}{a^2}u. \end{equation*}

Using the result from part (b) to eliminate \(u\) gives

\begin{equation*} u_S = \frac{a_h^2}{a^2}\sqrt{2gh}. \end{equation*}

We require \(u_S\) to be independent of time so that equally spaced intervals are traversed in equal times. Hence,

\begin{equation*} a=\left(\frac{a_h^2\sqrt{2g}}{u_S}\right)^{1/2} h^{1/4}. \end{equation*}

The terms in the brackets are constant, so we have that the radius of the jar must vary as the fourth root of the height.

🔗

Prev Top Next