Skip to main content

Exercises 2.3 Exercises

The kinematics chapter covered the basic essentials about the measurement and computation of fluid velocities and acceleration. We examined the difference between Eulerian and Lagrangian coordinates and derivatives. Examples of streamlines and velocity fields were examined.

Remark 2.3.1 Solutions and feedback.

Full solutions to these exercises can be found in the solutions to this chapter A.1 in Appendix A at the back of the book.
If you would like feedback on your work, the tutor will by default concentrate on the exercises highlighted with a yellow background in the online notes (the homework exercises), unless you specifically ask for feedback on a different exercise instead.

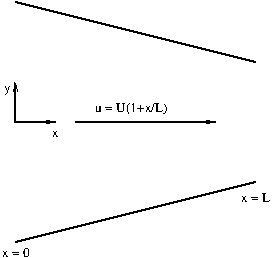
1. Flow visualisation.

Aside: Optional.

(a)

Name a few ways in which a fluid flow can be visualised (i.e. how does one produce, in an experiment, such a visualisation?)

(b)

Define, in words, what pathline, streakline, timeline, and streamline means. At 6:30, the author comments that "there is no way to make a streamline visible". Discuss this point.

(c)

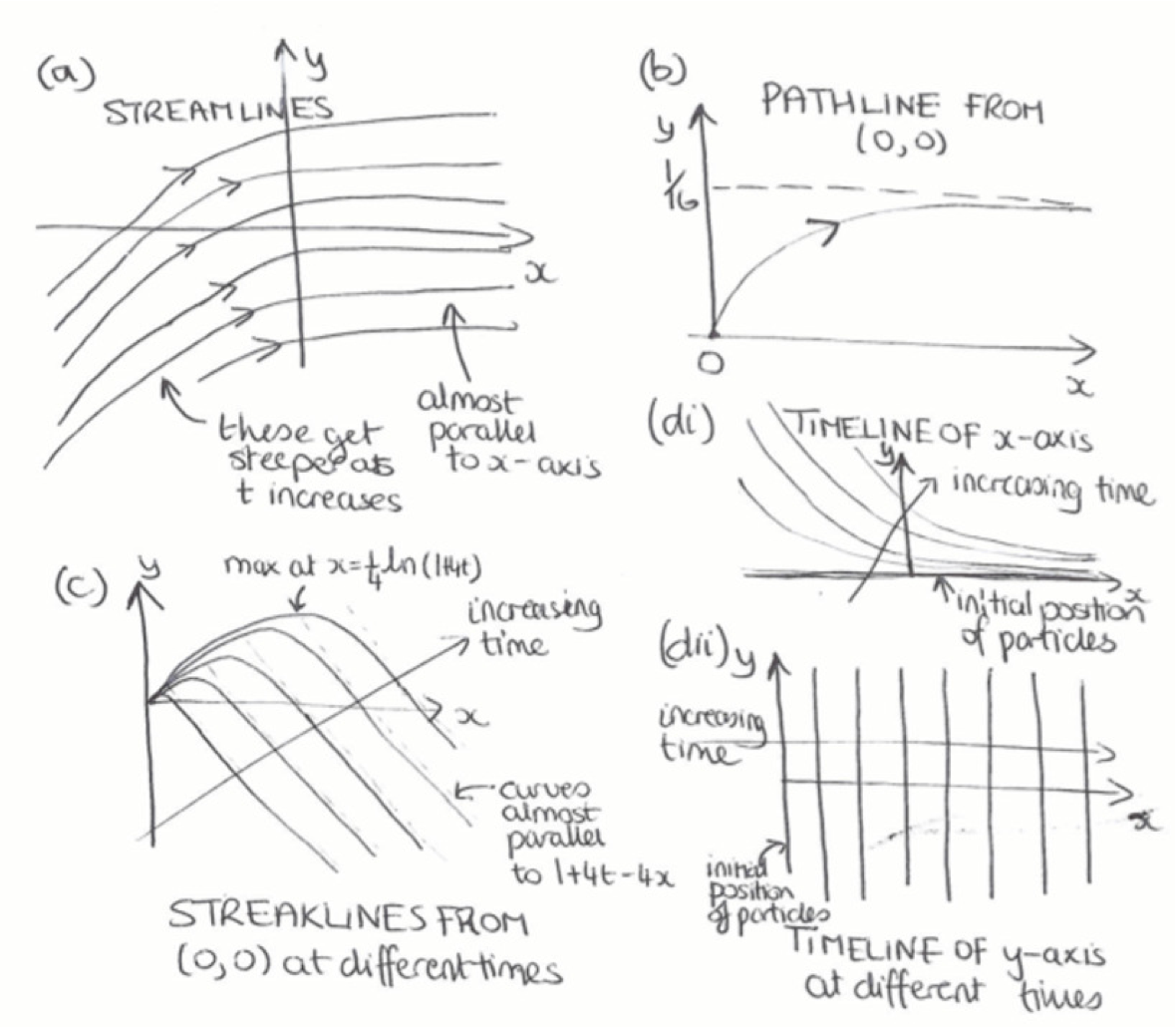
Give the example, shown in the video, where the pathline, streakline, and streamlines all coincide. Draw pictures to illustrate the concept.

(d)

Give an example, shown in the video, where the pathline, streakline, and streamlines do not coincide. Draw pictures to illustrate the concept.

(e)

In the video, an intuitive explanation is given for what it means for the velocity to be incompressible. What is this explanation? (near 8:25)

2. Derivation of the material derivative.

Prove the Eulerian representation of the material derivative, as presented in Theorem 2.1.5 by manually expanding the components of the function. That is, consider a scalar function \(f(\bx, t)\text{.}\) Let the spatial coordinate follow \(\bx = \bx(\bX,t)\) and hence is defined by a specified material label \(\bX\text{.}\) Then derive the identity for
\begin{equation*} \DD{f}{t} = \pd{f}{t} \biggr\rvert_{\bX}, \end{equation*}
according to Definition 2.1.3.

3. Eulerian and Lagrangian descriptions.

Aside: Revised in 2026.

A velocity field is described in Eulerian terms in Cartesian coordinates by \(\mathbf{u}=(-y,x)\text{.}\) What is the Lagrangian position of the particle that starts at the point \((x_0,y_0)\text{?}\) Describe its path. What is its velocity?

4. Eulerian and Lagrangian descriptions.

A fluid flows through the nozzle shown from \(x=0\) to \(x=L\) with one-dimensional velocity
\begin{equation*} u=U\left(1+\frac{x}{L}\right) \end{equation*}
in the \(x\)-direction, where \(U\) and \(L\) are constants. Note that, in reality the flow would be two- or three-dimensional, but we ignore this here for simplicity.
Figure 2.9. Sketch of nozzle.

(a)

What is the particle acceleration?

(b)

If a particle starts at \(x=0\) at time \(t=0\text{,}\) what is its position at time \(t\text{?}\)

(c)

What is its Lagrangian velocity as a function of time?

(d)

What is its Lagrangian acceleration as a function of time?

(e)

Write the Lagrangian velocity and acceleration as a function of \(x\text{.}\) Compare with the corresponding Eulerian velocity and particle acceleration. What do you notice?

(f)

How long does it take for a particle to travel from \(x=0\) to \(x=L\text{?}\)

5. Particle paths and streamlines.

Aside: Revised in 2026.

(a)

Define the particle paths and streamlines for a velocity field \(\bu(\bx,t)\text{.}\) When do these coincide?

(b)

Let \(\bx = \bx(t)\) be a pathline of the fluid, so that \(\dd{\bx}{t} = \bu(\bx(t), t)\) (see Definition 2.2.2), and consider \(f\) evaluated along the pathline,
\begin{equation*} F(t) = f(\bx(t), t), \end{equation*}
which is the value of \(f\) experienced by the fluid particle. By drawing a sketch of the pathline and marking the positions \(\bx\) of the particle at time \(t\) and \(\bx + \de\bx\) at time \(t + \de t\text{,}\) show that
\begin{equation*} \dd{F}{t} = \pd{f}{t} + \bu \cdot \nabla f = \DD{f}{t}. \end{equation*}
Hence show that \(f\) is preserved following the flow if and only if \(\DD{f}{t} = 0\text{.}\)
Hint.
Since \(\bx(t)\) is a pathline, the displacement of the particle in a small time \(\de t\) is
\begin{equation*} \de\bx = \bu(\bx, t) \, \de t + O(\de t^2). \end{equation*}
By definition of the derivative,
\begin{equation*} \dd{F}{t} = \lim_{\de t \to 0} \frac{f(\bx + \de\bx, t + \de t) - f(\bx, t)}{\de t}. \end{equation*}
To expand the numerator, use the Taylor series for a function of several variables:
\begin{equation*} f(\bx + \de\bx, t + \de t) = f(\bx, t) + \de\bx \cdot \nabla f(\bx, t) + \de t \, \pd{f}{t}(\bx, t) + O\big(|\de\bx|^2, \, |\de\bx| \, \de t, \, \de t^2\big), \end{equation*}
where, in components, \(\de\bx \cdot \nabla f = \de x \, \pd{f}{x} + \de y \, \pd{f}{y} + \de z \, \pd{f}{z}\text{.}\) Substitute for \(\de\bx\) and let \(\de t \to 0\text{.}\)

(c)

Let \(\bx = \bx(s, t)\) be a streamline of the flow at fixed time \(t\text{,}\) so that \(\pd{\bx}{s} = \bu(\bx(s, t), t)\text{,}\) where \(s\) is the parameter along the streamline (see Definition 2.2.1). Consider \(f\) evaluated on the streamline,
\begin{equation*} G(s) = f(\bx(s, t), t). \end{equation*}
Show that \(f\) is constant along the streamline if and only if
\begin{equation*} \bu \cdot \nabla f = 0. \end{equation*}
Hint.
Consider the points \(\bx = \bx(s, t)\) and \(\bx + \de\bx = \bx(s + \de s, t)\) on the same streamline, at the same instant \(t\text{.}\) Since the curve is a streamline,
\begin{equation*} \de\bx = \bu(\bx, t) \, \de s + O(\de s^2). \end{equation*}
By definition of the derivative,
\begin{equation*} \dd{G}{s} = \lim_{\de s \to 0} \frac{f(\bx + \de\bx, t) - f(\bx, t)}{\de s}. \end{equation*}
Because the time is the same at both points, the Taylor series now has no time term:
\begin{equation*} f(\bx + \de\bx, t) = f(\bx, t) + \de\bx \cdot \nabla f(\bx, t) + O(|\de\bx|^2). \end{equation*}

6. Streamlines, pathlines and streaklines.

The velocity of a two-dimensional fluid flow in Cartesian coordinates is \(u = 1\text{,}\) \(v = t e^{-4x}\text{.}\) Calculate and sketch the following:

(a)

the streamlines at a fixed time \(t > 0\text{,}\)

(b)

the pathline of the particle starting from \((x_0,y_0)\text{.}\) Hence find and sketch the pathline of the particle that starts from \((0,0)\text{,}\)

(c)

and the streaklines passing through \((0,0)\text{.}\)
Hint.
The expression for a general pathline starting from \((x_0,y_0)\) is given by
\begin{equation*} x = x_0 + t,\quad y = y_0 + \frac{1}{16} e^{-4x_0} - \frac{1+4t}{16} e^{-4(x_0+t)}. \end{equation*}

(d)

For a line/curve in the \((x,y)\text{,}\) its timeline at time \(t\) is the locus of the material elements at time \(t\) that started on the line/curve at \(t=0\text{.}\) In experiments this can be visualised using a streak of dye placed initally along the line/curve. Tracking this over time gives the timelines.
Calculate and sketch the timelines of the line (i) \(y=0\text{,}\) (ii) \(x=0\text{.}\)

7. An experiment for the material derivative.

Aside: Optional.

(a)

In the video, the authors describe an experiment that one can setup to measure decay of a substance, say \(C(x, t)\) along a 1D segment in a river.
In the first situation, it is assumed that \(C\) is distributed uniformly in the river, but is a naturally decaying substance with some uniform rate of change, \(\dd{C}{t}\text{.}\) Explain what is the (material) change in \(C\) that would be measured via two sensors, one upstream and one downstream.

(b)

Next, the authors imagine a situation where \(C\) is not uniformly distributed. They give a visual and analytical explanation of the material derivative,
\begin{equation*} \DD{C}{t} = \pd{C}{t} + u \pd{C}{x}, \end{equation*}
where \(u\) is the horizontal velocity within the infinitesimal 1D section. Write your own explanation of the above.
PrevTopNext